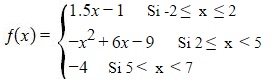Ayuda Rectas Parabolas Trozos

Se dan aquí las pautas para resolver los problemas que se plantean en este enlace

Advertencia: En el examen puede que no se de la gráfica o que no se de la fórmula por lo que debes dominar la representación gráfica de rectas y de parábolas y de hipérbolas )

Para calcular el dominio de f(x) hay que tener en cuenta que un punto del eje x es del dominio si existe f(x) y este es único.

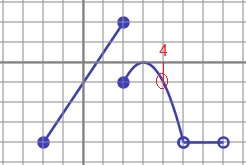
Domf=[-2 2)U(2 5)U(5 7)

En esta gráfica
El -3 no es del dominio pues ningún punto de la gráfica cae en x=-3
El 2 tampoco es del dominio pues hay dos puntos de la gráfica que caen en x=2, luego f(2) no está definida.
El 4, por ejemplo, si es del dominio pues f(4)=-1 (lo marcamos en rojo)
El 5 no es del domínio, la gráfica ahí aparece vacía
El 7 tampoco lo es

IMAGEN

La imagen queda determinada por la proyección de la gráfica en en eje de ordenadas o eje y o eje vertical

Imf=[-4 2]

En esta gráfica
Vemos su proyección sobre el eje de ordenadas en rojo, por tanto la imagen de f es el intervalo cerrado que va desde -4 hasta 2.

¿PARA QUÉ VALORES ES f(x)=-4?

En la gráfica anterior se observa que f(-2)=-4 y a la derecha para cualquier x entre 5 y 7 es f(x)=-4. Por tanto la respuesta es {-2}U(5 7), observar que en 5 y en 7 la función no está definida luego no vale 4 y hay que dejar el intervalo sin los extremos.

CONTINUIDAD EN UN PUNTO

Si una función es continua en un punto x, coinciden los límites laterales con el valor de la función en el punto: f(x^.)=f(x⁺)=f(x).
La continuidad de una función se puede ver sobre la fórmula de la función o sobre la gráfica

Estudio de la continuidad sobre la fórmula de la función
Veamos sobre la fórmula si f es continua en x=5

Calculamos f(5^-) al acercarnos a x=5 con puntos como 4,99, 4,999... y sustituyéndolos en la fórmula:

si nos acercamos a 5 por la izquierda, es decir a 5^- , estos valores de x ¿en qué tramo de la fómula de f(x) se encuentran? 4,99, 4,999... son menores que 5 y mayores que 2, por tanto estamos en el segundo tramo. Y si sustituimos ahí la x por 5 obtenemos -5²+6·5-9=-4

Por eso decimos que f(5^-)=-4

Análogamente se calcula f(5⁺) pero aquí los valores que se aproximan a 5 se toman con exceso, 5⁺ , 5,001, 5,0001, ..., estos valores de x están en el tercer tramo de la fórmula, es decir, entre 5 y 7, y vemos que en este tramo la función siempre vale -4
Concluimos que f(5^-)=f(5⁺) Sin embargo ya vimos que 5 no es del dominio porque la función no está definida en en x=5. f(5^-)=f(5⁺) pero no podemos completar diciendo que
f(5^-)=f(5⁺)=f(5)
porque este último valor, f(5), no está definido. Por tanto la función no es continua en x=5. Estos tipos de discontinuidades en las que coinciden los límites laterales se denominan discontinuidades evitables.

si nos acercamos a 2 por la izquierda, es decir a 2^- , estos valores de x ¿en qué tramo de la fómula de f(x) se encuentran? 1,99, 1,999... son menores que 2 y mayores que -2, por tanto estamos en el primer tramo. Y si sustituimos ahí la x por 2 obtenemos 1,5·2-1=3-1=2

Por eso decimos que f(2^-)=2

Veamos sobre la fórmula si f es continua en x=2

Calculamos f(2^-) al acercarnos a x=2 con puntos como 1,99, 1,999... y sustituyéndolos en la fórmula:

si nos acercamos a 2 por la izquierda, es decir a 2^- , estos valores de x ¿en qué tramo de la fómula de f(x) se encuentran? 1,99, 1,999... son menores que 2 y mayores que -2, por tanto estamos en el primer tramo. Y si sustituimos ahí la x por 2 obtenemos 1,5·2-1=3-1=2

Por eso decimos que f(2^-)=2

Análogamente se calcula f(2⁺) pero aquí los valores que se aproximan a 2 se toman con exceso, 2⁺ , 2,001, 2,0001, ..., estos valores de x están en el segundo tramo de la fórmula, es decir, entre 2 y 5. Sustituimos la fórmula de este segundo tramo por 2: -2²+6·2-9=-4+12-9=-1
Concluimos que f(2⁺)=-1
No se cumple que f(2-)=f(2+) luego la función no es continua en x=2. Al no coincidir los límites laterales se dice que la discontinuidad es de salto.

f(x) es continua en [-2 2)U(2 5)U(5 7)

Estudio de la continuidad sobre la gráfica de la función

Puede que a veces no tengamos la fórmula de la función, veamos como se estudia la continuidad de una función sobre su gráfica

Veamos sobre la gráfica si f es continua en x=5

Calculamos f(5^-) al acercarnos a x=5 desde su izquierda y viendo qué valores toma la función

Pulsa play para ver que si nos acercamos a 5 por la izquierda, es decir a 5^- , vemos sobre el eje de las ordenadas (y) que la función vale -4

Por eso decimos que f(5^-)=-4

Calculamos f(5⁺) al acercarnos a x=5 desde su derecha y viendo qué valores toma la función

Pulsa play para ver que si nos acercamos a 5 por la derecha, es decir a 5⁺ , vemos sobre el eje de las ordenadas (y) que la función vale -4

Por eso decimos que f(5⁺)=-4

Concluimos que f(5^-)=f(5⁺) Sin embargo ya vimos que 5 no es del dominio porque la función no está definida en en x=5. f(5^-)=f(5⁺) pero no podemos completar diciendo que
f(5^-)=f(5⁺)=f(5)
porque este último valor, f(5), no está definido. Por tanto la función no es continua en x=5. Estos tipos de discontinuidades en las que coinciden los límites laterales se denominan discontinuidades evitables.

Veamos sobre la gráfica si f es continua en x=2

Calculamos f(2^-) al acercarnos a x=2 desde su izquierda y viendo qué valores toma la función

Pulsa play para ver que si nos acercamos a 2 por la izquierda, es decir a 2^- , vemos sobre el eje de las ordenadas (y) que la función vale 2

Por eso decimos que f(2^-)=2

Calculamos f(2⁺) al acercarnos a x=2 desde su derecha y viendo qué valores toma la función

Pulsa play para ver que si nos acercamos a 2 por la derecha, es decir a 2⁺ , vemos sobre el eje de las ordenadas (y) que la función vale -1

Por eso decimos que f(2⁺)=-1

Concluimos que f(2⁺)=-1
No se cumple que f(2^-)=f(2⁺) luego la función no es continua en x=2. Al no coincidir los límites laterales se dice que la discontinuidad es de salto.

f(x) es continua en [-2 2)U(2 5)U(5 7)

DERIVADA DE f(x)

En todos los casos de estos problemas del enlace se puede derivar por tramos pero ponemos las desigualdades sin el signo igual, es decir desigualdades estrictas, ahora estudiamos a parte la derivabilidad de f en esos puntos de enlace, en 2 y en 5,

Para que exista la derivada en cada uno de estos puntos se han de cumplir dos cosas:

Que la función sea continua en ese punto
Que coincidan los límites laterales de f' en ese punto.

En nuestro caso la función no es continua ni en 2 ni en 5 luego no es derivable. f(x) es derivable en (-2 2)U(2 5)U(5 7)

Veamos la derivabilidad en otro ejemplo

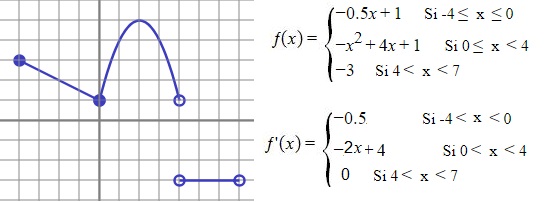
Aquí en x=0 la función si es continua pero no coinciden f '(0^-)y f '(0⁺): f '(0^-)= -0.5 y f '(0⁺)= 2·0+4 =4 Luego f no es derivable en x=0 (la derivabilidad también se aprecia a simple vista en la gráfica pues en x=0 la curva no es redondeada ni recta, tiene un pico).

En x=4 la función no es continua por tanto tampoco es derivable. Esta función es derivable en (-4 0)U(0 4)U(4 7)

La función de la siguiente figura es derivable en (-2 5)U(5 8), pues en x=2 que presenta el enlace de la recta con la parábola la función es continua y se une sin picos luego derivable. Esta función en x=5 no es continua presenta un salto y no está definida tampoco en x=5.

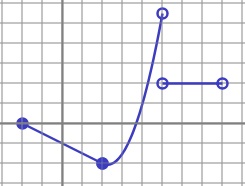
Se pueden ver más ejemplos actualizando sucesivamente la descarga de este enlace